Multiwfn的轨道定域化功能的使用以及与NBO、AdNDP分析的对比
文/Sobereva @北京科音
First release: 2017-Jun-5 Last update: 2019-Mar-17
摘要:本文首先介绍分子轨道定域化的含义,然后介绍在Multiwfn中做轨道定域化的基本步骤。然后通过5个例子,讲解如何基于定域化分子轨道讨论、分析体系的电子结构,并且与流行的AdNDP方法和NBO方法进行对比。本文的实例体现出轨道定域化的重要应用价值,也鲜明反映出NBO分析对于电子结构复杂、牵扯多中心离域的体系结果经常不靠谱,一定要慎用,最好不用。
我们做一般量子化学计算产生的分子轨道叫正则分子轨道(Canonical MO),它们是Fock或者KS算符的本征函数,本征值就是轨道的能量。下面说的MO都是指正则分子轨道。MO往往有很强的离域性,也就是说往往MO涉及很多原子,因此与化学键没法一一对应。所以,直接通过分子轨道讨论成键问题,多数情况毫无用处。有不少文章、毕业论文摆出来一堆MO图,但要么没怎么讨论(纯粹是凑数据),要么就是瞎讨论。例如,下面的图是丁烷的两个MO图,完全离域在整个分子。显然从这种MO图上根本没法直接对应众所周知的此体系存在C-C、C-H sigma键的事实。
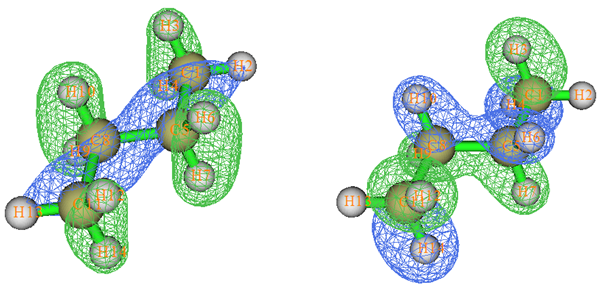
要想将轨道与化学键直接联系起来,需要做轨道定域化,将MO变换成定域化分子轨道(localized MO, LMO)。轨道定域化相当于对占据的MO做酉变换,从而产生出相同数目的离域程度尽可能低的占据轨道。描述体系波函数的Slater行列式无论是由原先的MO所构成,还是由变换后的LMO所构成,所对应的体系各种可观测量,如体系能量、电子密度、静电势等等,都是不变的。还有很多量虽然是不可观测的,但也不受这种变换所影响,比如电子定域化函数(ELF)。
通常做轨道定域化只需要把占据轨道定域化,因为可观测性质、成键问题等等都是只与占据轨道相联系。如果也想把空轨道做定域化,那么也可以再把空轨道以相同方式做酉变换来得到离域程度尽量低的空轨道。将空轨道做定域化主要是用于一些基于定域轨道的电子相关方法,比如知名的但如今用处不大的Local MP2 (LMP2)。由于空轨道比占据轨道数目多得多,将它们也定域化耗时会增加甚巨,而且空轨道对我们分析体系的性质没影响,所以通常我们只把占据轨道定域化就够了。
轨道定域化有许多做法。比较知名的是
(1)Edmiston-Ruedenberg定域化:1963年提出。通过最大化轨道的自互斥能(亦即最小化轨道间的互斥能)来实现定域化。缺点是耗时很高,而且得算复杂的双电子积分,而且又没额外好处,故很不推荐。
(2)Boys定域化:1960年提出。应用比较广泛,通过最小化轨道涵盖的空间范围来定域化。需要利用偶极矩积分。
(3)Pipek-Mezey定域化:1989年提出,它通过通过最大化Mulliken原子布居数的平方和达到定域化目的,编程实现颇为简单,只需要重叠积分,而且耗时很低,被广泛使用。后来还有人提出基于其它布居分析方法来做Pipek-Mezey定域化。
(4)NLMO定域化:NLMO的N是Natural的意思。这是NBO开发者提出的定域化方法,它将高占据(Lewis型)的NBO和低占据(non-Lewis型)的NBO以一定方式混合,从而得到整数占据的定域化轨道。由于得到NLMO轨道得先产生NBO,故此方法只有NBO程序,以及也同样能做NBO分析的Molpro才支持。
以上方法计算过程需要迭代,迭代过程中不同轨道间不断混合,最后使得目标函数被最大化或最小化。
不同的轨道定域化方法得到的LMO图形有一定差异。对于双键的描述,不同方法差异很大,比如下图是乙烯的C=C键,Pipek-Mezey产生的LMO保留了sigma和pi分离的特征,然而Boys定域化则是以两个香蕉键来描述这个双键。
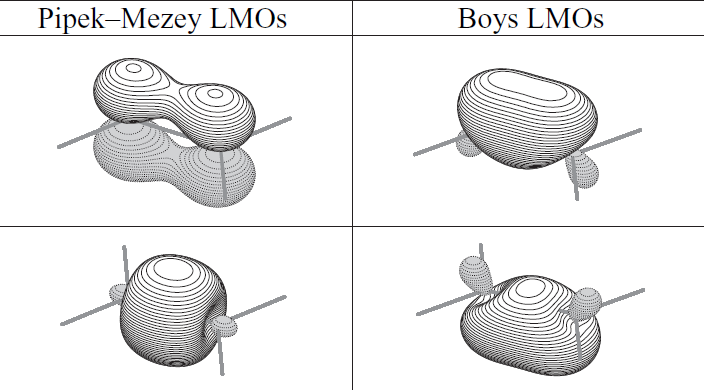
这两种双键的描述形式没法说谁对谁错,从物理角度上是等价的描述,但是显然Pipek-Mezey方法更好一些,结果更符合化学观念,更便于讨论。
Pipek-Mezey方法的一个缺点是不适合有弥散函数的情况,因为Mulliken布居在有弥散函数的时候结果缺乏意义。这点在《原子电荷计算方法的对比》()、《分子轨道成分的计算》()里面都谈过。不过近年来也有人提出基于IAO (Intrinsic Atomic Orbitals)代替原始基函数来做Pipek-Mezey定域化的做法(得到的轨道称为IBO),这使得弥散函数不会对结果有什么影响,因为IAO的意义和NBO框架中的极小集NAO很相似,从原始基函数变换成IAO的过程中已经把弥散函数的不良影响充分去除了。实际上,将其它不怕弥散函数的布居分析方法(如Hirshfeld、Becke)结合Pipek-Mezey方法使用也可以使定域化结果不会因为有弥散函数而受到不良影响。





